Momento de inercia

Cuando se analiza un movimiento traslacional y rectilíneo se considera a la masa del objeto como una medida de su inercia. Como ejemplo, si se aplica la misma fuerza a un camión y luego a un auto, observamos que el auto acelera más que el camión. En este caso, decimos que el auto cambia su estado de movimiento con mayor facilidad ante la fuerza aplicada. En términos técnicos, el auto tiene menos inercia que el camión.

Por lo tanto, la masa es una medida de la inercia de un cuerpo y es en este sentido, una medida de su resistencia al cambio de velocidad.

Análogamente, al hacer que un objeto sólido rote o se mueva en trayectoria curva, se observa una resistencia al cambio del movimiento rotacional. Esta oposición del objeto al cambio de su rotación se conoce como inercia rotacional o momento de inercia. En otras palabras, en el movimiento circular el momento de inercia cumple el mismo rol que la masa juega en el movimiento rectilíneo.

El momento de inercia lo encontramos en dos tipos posibles de sistemas:

Se trata de objetos físicos que modelamos como si se tratara de partículas que tienen toda su masa concentrada en un punto y que giran con la misma velocidad angular a cierta distancia de un eje de giro. Este es el tipo de sistema que consideramos cuando el eje de giro no atraviesa el objeto.

Por ejemplo, aunque para nosotros los planetas son enormes cuerpos masivos, su tamaño en relación al tamaño del Sistema Solar es en la práctica muy pequeño y por esta razón podemos modelar el movimiento de los planetas como si se tratara de partículas cuya masa se concentra en un punto.

Modelar a los planetas como partículas es una simplificación física importante, pero podemos lograr una muy buena aproximación a sus movimientos de esta manera.

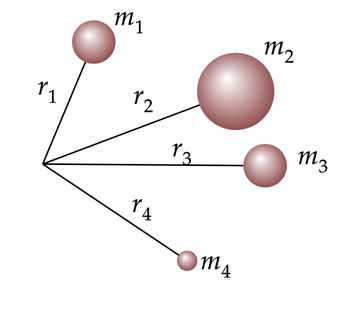
La inercia rotacional esta relaciona con la distribución de la masa respecto de un eje de giro. Para que un objeto inicie una rotación se requiere de una fuerza que actúa perpendicular al radio de giro, una vez que la masa inicie su movimiento, girará con una velocidad angular constante, esto se conoce como momento de inercia (I) y su unidad de medida es Kg m² . Cuando tenemos un sistema de partículas, podemos aproximar el cálculo del momento de inercia de la siguiente manera:

donde I es el momento de inercia para un sistema de partículas puntuales, m es la masa de cada partícula y r es la distancia de cada masa con respecto al centro de giro.  Esta relación indica que si varios objetos puntuales componen un sistema, el momento de inercia del sistema es la suma de los momentos de inercia de cada partícula respecto al mismo eje de rotación:

Se trata de objetos sólidos y rígidos que giran sobre un eje que atraviesa sus contornos. Son objetos rígidos aquellos que no experimentan deformaciones.

Ejemplos de objetos extensos en rotación hay muchos a nuestro alrededor. El caso más directo, aunque tal vez no el más evidente, es la propia rotación de la Tierra alrededor del eje imaginario que la atraviesa de polo a polo. Si lanzas un martillo al aire o haces girar un trompo, verás también cuerpos rígidos en rotación. Para calcular el momento de inercia de un objeto rígido no es posible usar la ecuación (Ec. 1) anterior directamente, ya que este tipo de cuerpo distribuye su masa en toda su extensión de distinta manera, de acuerdo a la geometría que posee.

Así, por ejemplo, un cilindro sólido tiene mayor momento de inercia que una esfera sólida del mismo radio y de igual masa.

En general, cada cuerpo geométrico, regular o irregular, tiene su propia inercia rotacional. La técnica matemática para calcular la inercia de objetos sólidos y extensos pertenece al área del cálculo diferencial e integral. Para evitar este tipo cálculos, a continuación se muestran algunos cuerpos geométricos comunes y sus respectivos momentos de inercia.

Paves, F., Jiménez, C., Ramos, M. (2009). Física 3º año medio. Santiago: McGraw-Hill/Interamericana de Chile Ltda.