Ondas Estacionarias
Superposición de ondas
Cuano dos o más movimientos ondulatorios alcanzan un mismo punto a la vez en el medio material por el que avanzan, se nos plantea el problema de saber que tipo de perturbación se experimenta en ese punto como consecuenciade las doas ondas que inciden sobre él. En el caso de los fenómenos ondulatorios, a estos se le denomina interferencia, que es el resultado de dos o más ondas del mismo tipo en un mismo medio.
Físicamente el principio de superposición se puede aplicar a pequeñas perturbaciones, en donde el efecto final es la suma de las elongaciones de cada una de las ondas por separado.
Interferencia Constructiva

La interferencia constructiva es la que nos proporciona un máximo, donde las dos amplitudes se suman, dando como resultado un pulso de mayor amplitud que los incidentes, pero que después cada uno sigue con su misma velocidad y dirección.
Interferencia Destructiva

La interferencia destructiva se produce cuando una dos pulsos viajan en sentido contrario pero desfasados en 90°, o sea uno va por la parte superior del medio y el otro por la inferior, de manera que al interferir las amplitudes de ambos se restan, dando como resultado un pulso de menor amplitud, que en el caso de ser de igual amplitud los pulsos incidentes, se anula por completo.
Interferencia

La interferencia en las ondas sonoras se produce cuando dos o más ondas sonoras coexisten en el mismo medio y al mismo tiempo, de modo que en cada punto del espacio se suman amplitudes o se restan.
Un ejemplo común de interferencia en ondas sonoras lo comprobamos al estudiar lo que ocurre cuando golpeamos simultánemaente dos diapasones o cualquier otra fuente sonora de frecuencia levemente diferentes. El sonido que se produce varía de intensidad, y alterna entre sonidos fuertes y silencio virtual. Estas pulsaciones regulares se conoce como pulsaciones o batido. El resultado es una onda de amplitud modulada generada por la oscilación.
Parece que las odnas sonoras se propagan sin afectarse unas a otras, incluso cuando su diferencia de intensidad es muy grande. Sin embargo, el sistema auditivo es sensible a la presión sonora total. Por lo tanto, es necesario analizar cómo se combinan o superponen diferentes ondas sonoras para encontrar la onda resultante de la superposición. esta corresponde a la suma algebraica de cada una de las elongaciones que componen a la onda.
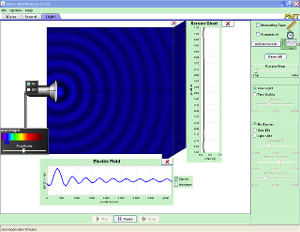
Animación Java
Animación que muestra la interferencia en ondas en el agua, del sonido y de la luz. En ella se pueden modificar como la cantidad de fuentes, o colocar una rendija y luego una doble rendija para donde cada punto se comporta como si fuera una fuente puntual en fase.
Para correr este tipo de animación necesitas instalar un programa que te permita ejecutar java script