Ondas estacionarias
Ondas Estacionarias en Instrumentos Musicales
Las ondas estacionarias nos permiten explicar cómo se produce el sonido en los instrumentos musicales y, además, ayudan a los fabricantes a trabajar de forma casi matemática en su construcción.
Las ondas estacionarias resultan de la interferencia y de la resonancia de ondas. Cuando ondas de igual amplitud y longitud de onda se interfieren en sentidos opuestos, se forman las ondas estacionarias, que a simple vista parecen inmóvil.

Los puntos donde interfieren de manera destructiva se denominan nodos y en los que interfiere de manera no destructiva antinodos. Es muy importante hacer notar que una onda estacionaria hay dos onda, por lo que por ejemplo en la figura superior hay:
- 3 nodos
- 2 antinodos
- 1 Ciclo completo, o sea un periodo completo (T) o una longitud de onda
Cuando una onda se refleja en una pared experimenta un cambio de fase en pi/2, o sea en medio ciclo, pues esta empuja la pared hacia arriba, entonces esta se opone y genera una fuerza de igual magnitud pero en sentido contrario, y por ello se devuelve por "abajo"
Ondas con ambos extremos fijos

Las ondas estacionarias con los extremos fijos son las que se dan en instrumentos de cuerda como guitarras, violines y pianos. Estos instrumentos constan de una o más cuerdas de longitud L, con una tensión determinada que permite seleccionar la frecuencia de su sonido.
Cuando se pulsa la cuerda sobre el mástil, disminuye la longitud de la cuerda y esto hace cambiar su frecuencia.
En las ecuaciones mostradas tenemos que:
v = rapidez de propagación de la onda en una cuerda mecánica.
T= Es la tensión de la cuerda medida en Newton
m= Es la masa de la cuerda medida en kilogramos
L= es la longitud de la cuerda medido en metros
f= es la frecuencia medida en Hz
λ= La longitud de onda medida en metros

¿Cómo se selecciona la frecuencia en los instrumentos musicales?
Suponemos que la longitud del medio, en este caso la cuerda es L, y debe cumplirse que en los extremos límites (condiciones de contorno) x=0 y x= L. Tiene que haber un nodo, es decir, una zona de ausencia de vibraciones o de mínima energía y un antinodo o punto donde la energía es máxima.
Des esta manera, la longitud de onda λ, de la primera onda estacionaria o primer armónico que se forma es:

En general tenemos:
- La frecuencia del modo enésimo es n veces la frecuencia del modo fundamental fn= n·fo
- La distancia entre dos nodos consecutivos es λ/2
- La distancia entre un nodo y antinodo consecutivo es λ/4
- La rapidez de la onda se mantiene constante, a menos que cambie la tensión.
- A mayor modo de vibración mayor frecuencia y menor longitud de onda.
Ondas con extremos libres

La mayoría de los instrumentos de viento son de extremos libres. La excepción la encontramos en los órganos, la flauta de pan o el clarinete.
Cuando una onda estacacionaria está confinada a un espacio con los dos extremos libres, coicide un antinodo con la zona abierta.
Las condiciones que se imponen es este caso es que tanto en x=0, como en x=L debe haber un antinodo. De esta manera nos damos cuenta que se cumple la misma condición que las ondas estacionarias con ambos extremos fijos, o sea λ = 2L.
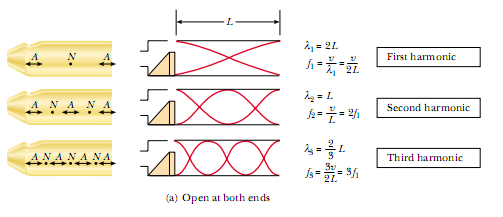

en un tubo con ambos extremos libres, las frecuencias de vibración natural forman una serie armónica, es decir, los armónicos más altos son múltiplos enteros del frecuencia fundamental.
NOTA: En la siguiente imágen se muestra ondas trasversales, sin embargo el sonido es una onda longitudinal, se ha hecho de esta menera porque es más gráfica y simple de entender que un dibujo de una onda longitudinal.
Ondas con un extremo fijo y otro libre

Cuando las ondas estacionarias están confinadas en un tubo con un extremo libre y uno fijo, como la zampoña, tenemos que x=0 y debe situarse un nodo, en cambio en x= L debe haber un antinodo.
Así el primer armónico encontramos que la longitud del tubo coicide con una cuarta parte de la longitud de la onda


El segundo armónico se produce cuando en el tubo hay tres cuartas partes de la longitud de onda.

Si nos fijamos en la imagen inferior, podemos llegar a la fórmula general para cualquiera longitud de onda de cualquier modo.

Por lo que la frecuencia del modo enésimo es:

